Introduction
I have been fascinated by the motifs on the stole of St Donats, Arlon, Belgium
(Collingwood 1982, p282; 12th century) for quite a while, but only a few months
ago gathered up the courage to try my hand at 3/1 broken twill. I decided that
a short piece such as a fillet would be a good item to try first, and combined
some of the ideas I had from the stole with heraldic images, which due to their
stylized nature lend themselves almost naturally to this style of weaving.
Research
Some of the earliest finds of patterned 3/1 broken twill date to the 6th century
(Collingwood 1982, p282). For the next several centuries the items found exhibit
increasingly complex motifs, well-known examples being the Maniple of St Ulrich
(10th century) and the Stole of St Donats (12th century). In some cases the
broken twill patterns are enhanced with brocading, and although this produces
some stunning results I decided the combination of twill and brocading would be
a bit beyond my scope at this stage.
The use of tabletweaving in various items of apparel is well-documented. Spies
provides an excellent overview of the uses to which bands were put (Spies 2000,
Appendix A), and there are historic finds of tabletwoven headbands and fillets.
Her analysis was conducted only on brocaded bands, but it is entirely plausible
that less wealthy folk would have used bands that did not contain expensive metal
thread in a similar fashion.
This is borne out by the finds of non-brocaded tabletwoven girdles and fillets
in a number of places in England (Crowfoot et al 2001, p130-133). The authors
make specific mention of six bands woven wholly from silk, 'produced in double-faced
weave'. Four of these bands are dated to the 14th century and two to the 15th,
and were apparently used as either fillets, girdles, or spur leathers.
One of the 14th century bands was definitely used as a fillet; the fragments found
were still attached to a false plait of hair. This band was woven plain-faced,
with a solid colour on each side. Another of the bands was woven with a
double-faced lozenge pattern, and from the photograph the fourth band looks like
it might be a type of hopsack with vertical stripes in alternating colours.
(See Appendix B for a photo of the bands).
I got excited for a moment with the third band because the catalogue summary
states that it is 'a double-faced weave with a diagonal twill effect'. Unfortunately
a close examination of the photograph reveals that the structure is clearly a basic
double-face with a solid colour on each side, not a 3/1 broken twill.
However, although I have not found any direct evidence of fillets woven in 3/1
broken twill, the existence of fillets woven using the closely related basic
double-face method leads me to believe that it is not unreasonable to assume that
someone, somewhere might have made a fillet in broken twill. I have thus attempted
to reproduce such a fillet using patterns and styles that would have been common
in 14th/15th century Anglo-Norman England.
Design and Weaving
Design: All designs are my own, based on period motifs and styles; more
specific information for each pattern can be found in the Pattern Details
appendix. I created them using my tabletweaving software (Guntram's Tabletweaving
Thingy); the design time ranged between 2 to 4 hours for each motif. I chose an
uneven number of tablets so that the central geometric pattern would be mirrored
evenly about its axis.
Material: Silk was a favourite material for those who could afford it; it
was both lightweight and strong. The fillets described by Crowfoot et al were
woven with quite fine silk thread, with 22 to 26 picks/cm; I used 60/2 silk as a
close approximation thereof (▒18 picks/cm).
Tools: A simple warp-weighted loom, a wooden beater and shuttle, and
cardboard tablets.
Method: I used the one-pack method for broken twill described by Collingwood.
I wish I could say that was because I think it is the proper period method (well,
I do think that), but actually I used it because it seemed the easier one to learn.
(And to be quite honest, I have not yet adapted my software to deal with the
two-pack technique, so I can only generate patterns for the one-pack method).
Weaving: Due to utter absent-mindedness I threaded all tablets Z instead
of S, but fortunately it was easy enough to adjust the patterns with my software.
Including warping, the whole weaving process took approximately 20 hours.
Finishing: As can be seen from the texture, I started and ended the fillet
using the basic double-face method. These ends are intended to be either cut off
or sewn under when it comes to finishing the fillet. I have intentionally left
the ends loose so that it easier to display the whole length of the band. Once
I have decided who to give the fillet to, the ends will be trimmed to the correct
length, folded over and sewn together to prevent fraying.
Um, Errors. Um.
Twill direction: When I designed the first set of patterns I did not realize how
the change in the twill direction would influence the pattern. Thus for the
first half (the right side) of the fillet the twill direction of the background
warp reverses itself on the left side of most of the motifs, and there are clear
marks where I idled tablets or made double turns to return the tablets to their
starting position so that I could start the next motif. Also, the twill lines
in the solid parts of the animals are not consistent but vary between S and Z twill.
Weaving errors: There are a couple of small weaving errors; counting from the
right (the side on which I started):
1. In the first tree, at the top of the trunk.
2. In the first bird, in the head and in the wing. I lost track of the tablet
positions and had to make some hasty adjustments.
3. In the second lion there is a gap in the front leg.
Band width: While I would not exactly call the 2mm width variation an error, it
is nonetheless a touch more than I could have wished for. I had not worked
properly with such fine thread before and it took me a while to adjust to it.
Technical Data
| Warp |
60/2 silk; red, blue, white |
| Weft |
60/2 silk; red |
| Width |
varies between 13mm and 15mm |
| Length |
615mm |
| Tablets |
37 four-hole tablets:
3 selvedge tablets on either side, alternately S and Z threaded. The outer
two tablets have been threaded with red silk in all holes, and the inner
tablet on each selvedge bears blue silk in all holes.
31 pattern tablets carrying blue silk for the background colour and white
silk for the pattern colour, all Z threaded.
|
| Patterns |
Various creatures alternating with trees and a geometric pattern in the
centre of the band, all in 3/1 broken twill.
|
Appendix A: Pattern Details
All pattern were designed specifically for this band by myself. I reversed each
of the animal patterns so that they can face either way, but I have included only
one version here due to space constraints. Full details of the patterns can be
found on my website http://users.mweb.co.za/e/ec/eckie/tabletweaving/.
Note: Well, this being my website I won't show the pattern details here but
just give a link to each pattern.
Notes
| 1 |
The line patterns show the turning sequence for the tablets, beginning on
the right hand side and working towards the left. The tablets must be
threaded for the one-pack method described by Collingwood.
 indicates a forward turn and indicates a forward turn and  a
backward turn. a
backward turn.
|
| 2 |
I used a horizontal rather than the usual vertical orientation of the patterns
here to conserve space. |
| 3 |
Although I wove the band using Z-threaded tablets (by accident more than
design), I decided to provide the patterns for a S-threaded warp, this being
the more commonly used method.
|
| 4 |
All images except for the heraldic pictures were produced by my software.
|
| Lion |
Design time: ▒4 hours
The original idea came from a section of a 8th/9th century band with a
border of lions (Collingwood 1982, Plate 166, p285). I also looked at
some brocaded animals for ideas, notably the lion on a 11th/12th century
chasuble attributed to St Wolfgang (Spies 2000, p120). I played around a
bit and eventually decided to try and create a lion couchant as depicted
in period heraldry.
I was not entirely happy with the first one I wove and made some small
alterations to the head for the second one (on the left side of the band).
The pattern below is for the second lion.
|
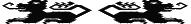
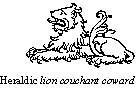
|
|
 Get the GTT pattern
here.
Get the GTT pattern
here.
|
| Bird |
Design time: ▒2 hours
This bird is based directly on one of the motifs in the stole of St Donats,
Arlon. (Collingwood Plate 173, p292). This is the pattern for the bird
facing towards the right.
|

|
|
 Get the GTT pattern
here.
Get the GTT pattern
here.
|
| Dragon |
Design time: ▒4 hours
I tried to produce a heraldic dragon statant with this pattern. Again the
first version was not quite satisfactory and I made some changes to the
head and tail. This is the pattern for the improved version.
|
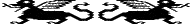

|
|
 Get the GTT pattern
here.
Get the GTT pattern
here.
|
| Tree |
Design time: ▒2 hours
This tree was vaguely influenced by the various tree motifs on the stole
of St Donats, but the final result turned out somewhat different from the
trees on the stole.
|
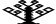
|
|
 Get the GTT pattern
here.
Get the GTT pattern
here.
|
| Geometric |
Design time: ▒3 hours
This pattern is based on the geometric patterns in the stole of St Donats.
I would have liked to produce a close replica of one of the motifs, but
due to the size constraints I settled for a loose derivative.
Note that I have not fixed this pattern yet - the twill direction at the
end is the opposite of the start.
|

|
|
 Get the GTT pattern
here.
Get the GTT pattern
here.
|
Appendix B: Period Pieces
|
Stole of St Donats, Arlon
Origin: Belgium, 12th Century
Material: Silk
Type: 3/1 Broken Twill
Source: Collingwood, Plate 169 (p288)
|
 |
|
English Silk Bands
Origin: England, 14th Century
Material: Silk
Type: various double-face
|
Pattern |
Tablets |
Width |
| A |
lozenge |
33 or 35 |
12mm |
| B |
plain |
12 |
8mm |
| C |
weft-wise stripes |
12 |
no data |
Source: Crowfoot et al, p133
|
 |
Bibliography
Collingwood, P. The Techniques of Tabletweaving. London 1982.
Crowfoot, E., Pritchard, F., Staniland, K. Textiles and Clothing: 1150 - 1450.
London 2001.
Hansen, E. Brikvævning. H°jbjerg 1990.
Spies, N. Ecclesiastical Pomp & Aristocratic Circumstance: A Thousand Years of
Brocaded Tabletwoven Bands. Jarretsville 2000.
Judges' Comments
This is a compilation of some of the judges' comments, together with my response.
| Comments |
My Response |
|
I would have liked to know some more about the colours you chose.
-
Excellent documentation, covers all you want to know except that I would
have liked some more information on colours normally used and the choice
of colour.
-
The blue is a little iffy.
|
Looks like this was a concern of all the judges. It is not apparent in the
scan, but the blue is actually quite bright, with a touch of turquoise. (My
scanner is really bad at picking up colours). With hindsight I have to
agree that the blue is not right; I think a better period colour would have
been a darker, more heraldic blue.
|
|
|
What is 3/1 broken twill? With this I mean that sometimes you were a little
too advanced :) but hey, you squeezed it in on three pages.
|
Next time I'll use a smaller font. :) Yes, I probably should have given a
brief structural description.
|
|
|
I gave you slightly lower points because I was unsure of whether or not the
threading should have been S instead of Z to be entirely correct.
|
I'll keep that in mind; I should probably have been clearer on the fact that
both S and Z twill were used in period.
|
|
|
It would be interesting to know how easy or difficult you found it to be
using silk thread.
|
I love this question. :) Silk is my absolutely favourite material; it is
light but very strong, does not stretch, there's virtually no abrasion from
turning the cards, and of course it is perfectly period.
|
|
|
I'm sure you're right about someone using the 3/1 twill in a fillet
somewhere but... no examples...
|
True, no examples. I feel fortunate though that I came up with a fillet
in doubleface at all; research into historic tabletweaving is a rather
esoteric subject. Examples of period finds are not too extensive, and most
bands that have been found were brocaded - it is usually the metal that
survived, rather than the fabric itself.
|
|
The points are a bit lower because of the use of a computer generated
pattern.
-
The use of a computer program pulls it down a bit but it's certainly time-saving. :)
|
Hm, I think I have to argue this point. The patterns were not generated by
a computer, they were generated by me; the software is simply a tool that
makes the design process a little bit easier, much like typing out the
wording of a scroll before doing the actual calligraphy. Designing a
pattern is the same whether it's done on a computer or a piece of paper;
the main advantage of doing it on a computer is that playing around with
the pattern and making changes is much easier.
Also, since I wrote the program myself, it is based entirely on my own
knowledge of tabletweaving, thus any help provided by the program is of my
own making.
If that won't convince any judges, then I guess I'll have to live with
lower scores. :)
|
Occasionally maintained by Eckhard Gartz.
Last modified 5/5/2004.


 indicates a forward turn and
indicates a forward turn and  a
backward turn.
a
backward turn.
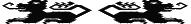
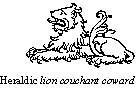
 Get the GTT pattern
Get the GTT pattern 
 Get the GTT pattern
Get the GTT pattern 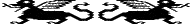

 Get the GTT pattern
Get the GTT pattern 
 Get the GTT pattern
Get the GTT pattern 
 Get the GTT pattern
Get the GTT pattern 
